Cracking The Coding Interview(코딩 인터뷰 완전분석)를 참고하여 작성하였습니다.
트리
- 트리는 노드로 이루어진 자료구조이며 사이클이 존재할 수 없다.
- 트리에서의 탐색은 최악의 수행 시간과 평균 수행 시간이 크게 다를 수 있으므로 주의가 필요하다.
트리 vs 이진트리
- 이진트리는 각 노드가 최대 두 개의 자식을 갖는 트리
- 즉 모든 트리가 이진트리는 아니다.
이진 트리 vs 이진 탐색 트리
- 이진 탐색 트리는 [모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들]을 만족해야 한다.
- <=이 <이 될 수도 있다.
- 트리 문제에서 모두가 이진 탐색 트리라고 생각은 금물!
균형 vs 비균형
- 많은 트리가 균형적이나 그렇지 않은 트리도 많다. 문제를 풀 때 확실히 인지하자
- 균형 트리의 대표는 레드-블랙 트리, AVL 트리가 있다.
완전 이진트리
- 마지막 레벨을 제외한 모든 노드가 꽉 차있고 마지막 레벨은 노드가 왼쪽에서 오른쪽으로 채워진 트리
- 마지막 레벨에서 왼쪽엔 노드가 없는데 오른쪽에 있으면 완전 이진트리가 아니다!
전 이진 트리
- 모든 노드의 자식이 없거나 정확히 두 개 있는 트리
- 즉 자식이 하나인 트리가 존재하지 않는다.
포화 이진트리
- 이진트리이면서 모든 노드가 꽉 차 있는 트리
- 2^n - 1 개의 노드가 존재, (n은 트리의 높이)
이진트리 순회
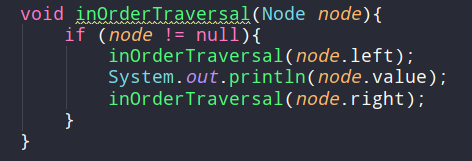
중위 순회(in-order traversal)
- 왼쪽 -> 현재 -> 오른쪽 순서로 방문하는 것
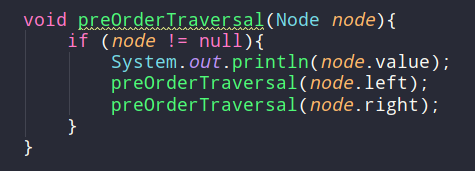
전위 순회(pre-order traversal)
- 현재 -> 왼쪽 -> 오른쪽 순서로 방문하는 것

후위 순회(post-order traversal)
- 왼쪽 -> 오른쪽 -> 현재 순서로 방문하는 것
이진 힙(최소 힙, 최대 힙)
- 최소 힙만 이야기하고 최대 힙은 그 반대로 생각
- 완전 이진트리이면서 부모 노드의 값이 자식 노드의 값보다 작거나 같을 때 최소 힙이라고 한다.
삽입
- 삽입 시 완전 이진트리를 유지하기 위해 마지막 레벨에서 놓을 수 있는 가장 왼쪽에 값을 넣는다.
- 부모랑 비교해서 값이 더 작으면 바꾼다. -> 이걸 반복한다
- 노드의 개수가 n이면 높이는 logn이므로 삽입의 시간 복잡도는 O(logn)이다.
최소 원소 뽑아내기
- 첫 번째 노드를 뽑아낸다
- 가장 끝에 있는 노드랑 첫 번째 노드랑 swap 한다. 그러면 가장 끝에 있는 노드가 가장 작은 노드가 된다.
- 그 노드를 뽑아내고 사이즈 하나를 줄인다.
- 그리고 첫 번째 있는 노드를 자식들과 비교해가면서 자리를 찾는다
- 결국 자리를 찾는 건 높이보다 클 수 없으므로 O(logn)이면 충분하다.
트라이(접두사 트리)
- n-차 트리의 변종으로 각 노드에 문자를 저장하는 자료구조이다. 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다
- null node라고 불리는 * 노드로 단어의 끝을 알 수 있다.
- null node는 다양한 방식으로 구현 가능, boolean flag나 TerminatingTrieNode 같은 상속 노드를 만들면 된다.
- 트라이를 사용하면 접두사를 O(K) 시간에 빠르게 찾을 수 있다.
- 해시 테이블도 O(K)이다. O(1) 같지만 문제열을 전부 읽어야 하는 시간이 문자열의 길이 K이기 때문이다.
- 현재 노드를 참조값으로 넘길 수 있어 단어들을 조회할 때 유용하다.
그래프
- 트리는 그래프의 한 종류이다. 하지만 모든 그래프가 트리는 아니다.
- 그래프는 단순히 노드와 그 노드를 연결하는 간선을 하나로 모아놓은 자료구조이다.
- 그래프는 양방향 일수도 단방향일 수도 있다.
- 그래프는 사이클이 존재할 수도 사이클이 없는 '비 순환 그래프' 일 수도 있다.
실제 표현방법
인접 리스트
- 그래프를 표현할 때 가장 일반적인 방법
- 모든 정점(노드)을 인접 리스트에 저장한다.
- 저장공간은 노드의 개수 M과 에지의 개수를 N이라 하면 O(M + 2N) -> O(M + N)이다
- O(M + 2N)인 이유는 에지는 서로서로 가지고 있기 때문이다.
- 어떤 u의 인전 한 노드를 찾는 시간 복잡도는 O(degree(u))이다. degree는 그 노드의 간선의 개수
- 어떤 에지 u, v를 찾는 것도 O(degree(u))가 된다.
인접 행렬
- 인접 행렬 N x N으로 구현 가능
- [i][j]에 값이 존재하면 i -> j에 간선이 존재
- 무방향 그래프일 시 대칭 행렬이 된다.
- 저장공간은 O(M^2)이 된다.
- 어떤 노드에서 인전 한 노드를 찾을 때 O(M)이 된다
- 어떤 에지 u, v를 찾는 건 O(1)이 된다.
그래프 탐색
깊이 우선 탐색(DFS, Depth-First Search)
- 구현하기가 조금 더 간단하다.
- 한 노드에서 연결된 노드를 계속 타고 들어가면서 탐색하고 더 이상 탐색할 게 없으면 빠져나오면서 반복 탐색

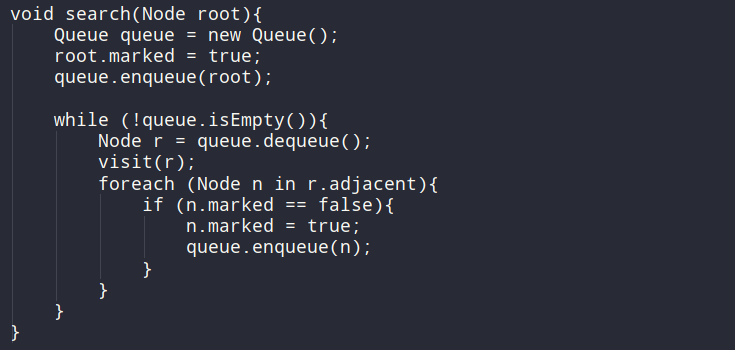
너비 우선 탐색(BFS, Breadth-First Search)
- 최단 경로나 임의 경로를 찾을 땐 DFS보다 일반적으로 좋다.
- 한 노드에서 인접한 노드 순으로 탐색하는 것이다.
- 실제로 큐로 구현된다!
양방향 탐색
- 출발지와 도착지 사이의 최단 경로를 찾을 때 사용되곤 한다.
- 일반적인 너비 우선 탐색으로 찾는 거보다 짧은 시간 복잡도로 구현 가능하다.
- A -> B로 가는 최단 경로가 D라고 생각하자. 각 노드는 적어도 N개의 이웃 노드가 연결되어있을 때 A에서 너비 우선 탐색을 시작해 B까지 가는 시간 복잡도는 O(N^D)가 된다.
- 하지만 양방향 탐색으로 하면 중간지점에서 충돌하게 되므로 O(2* N^(D/2)) -> O(N^(D/2))가 된다.
문제
코드: https://github.com/DongmyeongLee22/Algorithm/tree/master/src/com/company/cracking/treeAndgraph
노드 사이의 경로
- 방향 그래프가 주어졌을 때 두 노드 사이의 경로가 존재하는지 확인하기
- BFS, DFS로 구현하면 된다.
- visit 체크하는 건 기본이다. BFS, DFS 장단점에 대해 이해하자.
최소 트리
- 오름차순으로 정렬된 배열이 있고, 값은 정수이며 중복 값이 없을 때 높이가 최소가 되는 이진 탐색 트리 작성
- 왼쪽 하위 트리, 오른쪽 하위 트리의 개수를 최대한 같게 하면 높이가 최소
- 루트 노드는 배열의 중간에 있는 값
- 배열의 시작 ~ 중간 - 1은 왼쪽 하위 트리, 중간 + 1 ~ 끝은 오른쪽 하위 트리다.
- 이렇게 나뉜 트리도 이진트리이므로 나뉜 배열의 중간에 있는 값이 나뉜 트리의 루트가 된다.
- 이것을 재귀적으로 구현하면 된다.
- 만약 이렇게 하지 않고 하나하나 삽입하면 전체 노드수 N이고 위치 찾는 시간이 logN이므로 O(NlogN)이다.
깊이의 리스트
- 이진트리가 있을 때 각 레벨별로 리스트를 만들어라
- 너비 우선 탐색으로 해도 되지만 순회 방식도 가능
- 너비 우선 탐색은 일반적인 방법으로 구현하면 된다.
- pre-order traversal로 구현할 수 있는데 함수 매개변수에 level 넣어서 비교해가면서 넣을 수 있다,
- 둘 다 O(N) 시간이 든다. 모든 노드를 탐색해야 하므로..
- 순회 방식은 재귀 호출로 스택이 쌓여 O(logN)이나 BFS는 없음.
균형 확인
- 이진트리가 균형이 잡혀있나?
-> 모든 노드에서 왼쪽 트리와 오른쪽 트리의 레벨 차이가 최대 하나일 경우 균형적이라고 한다.
- 높이를 구하는 함수를 만들어 사용하면 된다.
- left, right의 높이를 재귀적으로 구하면서 만약 높이차이가 1 이상 나면 어떤 특정한 값을 반환하게 한 후 결괏값이 그 특정한 값이면 false, 그렇지 않으면 true로 구현하면 된다.
- 단순히 전체 트리를 재귀적으로 구현하면 O(NlogN)이나 위의 방법을 쓰면 O(N)에 가능하다.
BST 검증
- 이진 탐색 트리의 특징인 왼쪽 노드는 부모 노드보다 작고, 오른쪽 노드는 부모노드보다 큰 성질을 이용하면 된다.
- Node, min, max를 파라미터로 가지는 함수를 만들어서 재귀 구현하면 된다.
- min, max는 초기값을 null로 두기 위해 Integer 타입으로 한다.
- 현재 노드의 값이 min 보다 작거나, max보다 크면 false를 retrun 하면 된다.
- 재귀 알고 리즈 구현이 base case와 null case를 잘 생각해야 한다.
후속자
- in-order traversal 시 어떠한 노드가 주어졌을 때 다음 노드를 찾기. left, rigt, parent 링크 존재
- in-order traversal은 왼쪽 -> 자신 -> 오른쪽이다. 이것을 생각하면서 다음 노드가 어디에 있는지 생각해보자.
- 어떤 노드가 주어졌을 때 만약 오른쪽에 자식이 있다면 그 오른쪽 자식 중에 가장 왼쪽에 있는 노드가 다음 노드이다.
- 만약 오른쪽 자식이 없다면 부모 노드가 자신의 왼쪽에 있나 오른쪽에 있냐가 중요하다.
- 만약 내 부모 노드가 나의 오른쪽에 있다면 그 노드가 다음 노드가 된다.
- 내 부모 노드가 나의 왼쪽에 있다면 그 노드는 순회가 된것이므로 위로 올라가면서 부모노드가 오른쪽에 있을때까지 반복 하면 된다.
- 부모노드가 오른쪽에 있는 경우가 없는 노드는 트리에서 가장 오른쪽 하단에 있는 노드뿐이므로 그때는 null을 반환하면 된다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| 비트 조작 #1 (0) | 2019.12.27 |
|---|